פלוסים ומינוסים

פרק 1
המתמטיקה מקיפה אותנו מכל עבר

בכל פעם שאתם משתמשים במפות גוגל כדי למצוא את הדרך למקום כלשהו, אתם מסתמכים על סוג כלשהו של חישוב מתמטי. אתם פותחים אפליקציה, מקלידים את היעד שלכם, ובתוך שניות ספורות האפליקציה תציע לכם כמה מסלולים אפשריים. גוגל יכול לעשות זאת רק באמצעות שימוש מתוחכם במתמטיקה.

דמיינו לכם שגוגל היה נתקף טירוף ומטיל על אנשים שמצטיינים בקריאת מפות לתכנן את המסלול שלכם. בכל פעם שתחפשו מסלול נסיעה, הם יושיבו את האנשים האלה אל שולחן העבודה. לא זו בלבד שהדבר יגזול זמן רב, הוא גם יהיה בלתי יעיל לחלוטין. קוראי המפות של גוגל יצטרכו לשוב ולתכנן פעם אחר פעם אותו מסלול למען אנשים כמוני שאינם מסוגלים לזכור כמה זמן יידרש להגיע מביתם לבתים של חבריהם. במקרה הטוב הם יתכננו מסלולים שונים מראש, למקרה שמישהו יזדקק להם ביום מן הימים.

אבל האם כך יהיה טוב יותר? הסיכויים שמישהו זקוק לאותו מסלול בדיוק כמו זה שאתם זקוקים לו אינם גדולים, אלא אם למשל אתם גרים במעונות סטודנטים ומחפשים את הדרך הטובה ביותר אל האוניברסיטה. השכנים שלי בוודאי לא ילכו לבקר את החברים שלי או את המו״ל שלי, שאת כתובתו אני מעלה בכל פעם מחדש ביישומון, כי אני צריך לוודא, שוב, שאגיע אליו במועד שקבענו. כל עוד גוגל אינו יכול לִצפות לאילו נסיעות אני עתיד לצאת, הוא יזדקק בקביעות למישהו שיתכנן מסלולים חדשים. ואל לנו להשלות את עצמנו, טובים ככל שיהיו מתכנני המפות, הדבר תמיד יגזול זמן רב.

לכן אנחנו מפקידים את קריאת המפות בידי המתמטיקה. המחשב מוצא בשבילכם את הדרך הטובה ביותר שבה תיסעו, אבל לא באותו אופן כמו שעושים זאת בני אדם. המתמטיקה שהמחשב משתמש בה אינה מזהה רחובות בצילום לוויין ואינה יכולה לחשב מרחקים על פי קנה המידה של מפה. מערכות ניווט רואות את העולם כאוסף של מעגלים קטנים המחוברים ביניהם בקווים. מוזר ככל שזה נשמע, הרעיון יהיה מוכר לכל מי שראה מפה של קווי רכבת תחתית, כמו זו של לונדון באיור הבא.

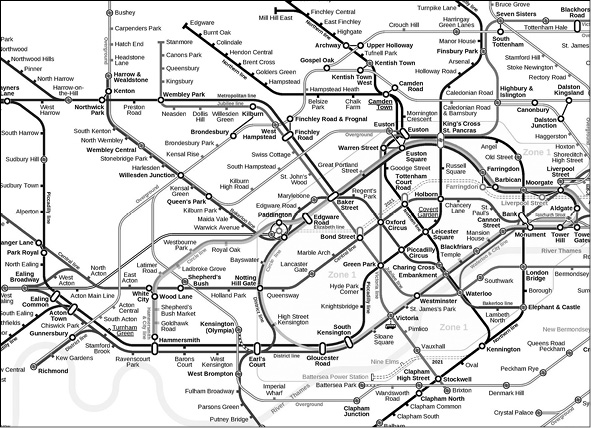
מפת הרכבת התחתית של לונדון¹

בשביל מפות גוגל, המצב האידיאלי הוא אם אתם נוסעים רק ברכבת התחתית, שכן המפה כבר מתוכננת באופן שתואם למתמטיקה של היישום. המחשב יכול להעמיד פנים שהוא נוסע לאורך הקווים בין המעגלים, כמו רכבת וירטואלית. הבעיה היחידה של המחשב היא שהוא אינו יכול לראות את הרשת כולה. אם אתם רוצים לתכנן נסיעה מהולבורן (שם הקו האדום והקו הכחול הכהה מצטלבים במרכז לונדון) לתחנת סבן סיסטרס (על הקו הכחול הבהיר באזור 3, לכיוון מזרח), אתם יכולים למצוא את דרככם במהירות רבה. הקו הכחול הכהה והקו הכחול הבהיר עוצרים שניהם בתחנת פינסברי פארק, ממש לפני סבן סיסטרס. לכן הדרך הטובה והמהירה ביותר היא לנסוע לפינסברי פארק בקו הכחול הכהה ומשם לנסוע מרחק תחנה אחת בקו הכחול הבהיר לתחנת סבן סיסטרס.

המחשב לעומת זאת, צריך לעבור הליך נפתל הרבה יותר כדי לחשב את המסלול הקצר ביותר. הוא אינו יודע איפה נמצאות התחנות הולבורן ופינסברי פארק האחת ביחס לאחרת, ולכן הרכבת הווירטואלית שלו נאלצת לנסוע סחור־סחור באופן אקראי עד שהיא מגיעה בסופו של דבר ליעדה. יתר על כן, המחשב צריך לדעת כמה זמן נדרש לרכבת לנסוע ממעגל קטן אחד לזה שאחריו. כפי שכולנו יודעים, המרחקים לאורך קווי הרכבת שנראים במפה אינם מייצגים את המרחקים האמיתיים מתחנה אחת לאחרת. נדרש קצת פחות זמן לנסוע מפארק רויאל לאלפרטון (על הקו הכחול הכהה האנכי לכיוון מערב) מאשר מפארק רויאל לנורת אילינג (שלוש דקות לעומת ארבע), ואילו על המפה תחנת אלפרטון נראית רחוקה הרבה יותר.

הפתרון לבעיה הוא להציב לצד כל קו בין התחנות ברשת מספר המציין את הזמן שנדרש לרכבת לעבור את קטע הדרך ביניהן. המחשב יכול להשתמש במספרים האלה כדי למצוא את המסלול הטוב ביותר. אחת ממערכות הניווט הפשוטות ביותר תסתכל בכל המסלולים השונים המתחילים בהולבורן, החל במסלול הקצר ביותר האפשרי, אחר כך במסלול השני הקצר ביותר וכן הלאה.

אם כך, בדוגמה שלנו המחשב מתחיל בהולבורן ומחפש את התחנה הקרובה ביותר. תחנת צ'אנסרי ליין ותחנת ראסל סקוֵור נמצאות שתיהן במרחק דקה אחת בלבד, לכן כל אחת מהן יכולה להיות הבחירה הראשונה. האם המחשב ממשיך מראסל סקוור לקינג'ס קרוס או מצ'אנסרי ליין לסנט פול? לא, הוא עושה ניסיון נוסף לנסוע בכיוון קובנט גרדן, שכן דרך זו קצרה יותר מהנסיעה לקינג'ס קרוס או לסנט פול. ואז הוא מסתכל על אוקספורד סטריט, המרוחקת שלוש דקות מתחנת הולבורן. רק לאחר שהמחשב בחן את כל האפשרויות האלה, הוא מתקדם לתחנה השנייה שאחרי הולבורן בכיוון סבן סיסטרס.

בדרך זו המחשב מקדיש זמן רב למדי כדי להגיע בסופו של דבר לסבן סיסטרס, מסע של 22 דקות שעוברים בו על פני שבע תחנות. אבל לפני שהוא מגיע לשם, הוא כבר עבר בבריקסטון, תשע־עשרה דקות בלבד בצד התחתון של מרכז המפה, ובתחנת אדג'וֵור, שהדרך אליה קצרה יותר, שבע־עשרה דקות, במרכז החלק העליון. אבל הוא מגיע ליעד בסופו של דבר, ומהשנייה שבה מצא את סבן סיסטרס, המחשב בטוח שהמסלול הראשון שחישב הוא הקצר ביותר. כל זה נשמע בלתי יעיל בעליל, וחוש הכיוון של האדם ויכולתו לראות את כל התמונה במבט כולל נראים פשוטים הרבה יותר. ובכל זאת, המחשב מהיר יותר מאיתנו רק מפני שהוא יכול לחשב מספר צעדים גדול הרבה יותר בכל שנייה נתונה.

היישומון של מפות גוגל עובד בדרך דומה למדי. המעגלים הקטנים אינם תחנות אלא צמתים, כגון מעגלי תנועה או הצטלבויות כבישים. מבחינת המתמטיקה, יש הבדל אם קו מייצג כביש ראשי או רחוב צדדי. כמו בדוגמה של מפת התחתית, הכול תלוי במידע שמספקים על משך הנסיעה, מידע המבוסס על המספרים שהיישומון של גוגל מציב לצד כל קו. קטע של כביש ראשי או של רחוב צדדי יכולים להיות באותו אורך, אבל ברחוב צדדי חייבים לנהוג לאט הרבה יותר, ולכן במערכת של היישומון, המספר המסמן את הרחוב גדול הרבה יותר מזה שמסמן את קטע הכביש הראשי. המספרים עוזרים גם להתאים את משך הנסיעה למידת העומס בכבישים. כל מה שנדרש מגוגל זה להגדיל את המספר שלצד הכביש העמוס, נניח מעשר דקות לעשרים דקות, כדי להביא בחשבון את העיכוב הצפוי של עשר דקות. אם אתם מחשבים מחדש את המסלול שלכם, העיכוב ייכלל באופן אוטומטי בזמן הנסיעה במסלול החדש. ייתכן שהנווט יכוון אתכם לכבישים צדדיים כדי לעקוף את הפקק, מפני שמסלול שבתחילה נראה ארוך יותר, הוא עכשיו מהיר יותר.

רשת כבישים כפי שאפליקציית גוגל מפות רואה אותה²

השיטה הזאת עובדת היטב במרחקים קצרים, אבל אם רוצים לנסוע למרחקים גדולים יותר, המתמטיקה נעשית בלתי אפשרית מרוב סרבול. אם רוצים לנסוע במכונית מניו יורק לשיקגו, גוגל מריץ תחילה את כל המסלולים האפשריים מניו יורק שאורכים פחות משתים־עשרה שעות (הזמן הדרוש לנסיעה). מחשבים מסוגלים לחשב מהר מאוד, אבל אפילו מחשב מודרני אינו יכול לעשות חישובים רבים כל כך בזמן קצר. לכן האפליקציה משתמשת במספר טריקים מתמטיים כדי להפחית את מספר החישובים. איננו יודעים מהם בדיוק, שכן גוגל שומרים בסוד את השיטות שלהם, אבל נתבונן בהם בפירוט רב יותר בפרק 7.

כפי שראינו, המסלולים שמערכות הניווט ממליצות עליהם מלאים כולם במתמטיקה. אבל המתמטיקה הזאת אינה בהכרח חכמה יותר מאיתנו. החיפוש הנואש של המחשב אחר היעד הסופי במקרים רבים רחוק מאוד מלהיות יעיל. המתמטיקה אינה הופכת את הבעיה לפשוטה יותר, מפני שבסופו של דבר המחשב נאלץ לעבוד יותר מאיתנו, אבל היא בהחלט מקילה את חיינו. היא יכולה למצוא את המסלול הטוב ביותר במהירות רבה יותר רק בגלל שהמחשב מסוגל לחשב מספר מדהים של חישובים מדי שנייה.

המלצות לצפייה בנטפליקס
אחרי שהטלתם על גוגל לחשב באיזה מסלול כדאי לכם לנסוע, אתם מדפדפים בחיפוש אחר סרטים חדשים בנטפליקס. לצד שמו של כל סרט מוצג בצבע ירוק מספר באחוזים שאומר לכם עד כמה הסרט הזה דומה או קרוב בסגנונו לסרטים שאתם צופים בהם בדרך כלל. לפעמים המספר הזה שגוי לגמרי, והסרט שאתם אמורים לחשוב שהוא נהדר מתגלה כאכזבה גדולה, אבל אם לשם שינוי לא תתעלמו מהאחוזים, הם עשויים לשקף את טעמכם בדייקנות רבה. ההמלצות נוצרות באופן אוטומטי לגמרי, והן ישתנו ככל שתִצפו בתוכניות מסוגים שונים. במילים אחרות, יש תוכנת מחשב אי־שם שיודעת, בלי שיהיה לה שמץ הבנה בסרטים או בסדרות, מה מתאים לטעמים שלכם ומה לא.

בנטפליקס עושים זאת כמובן על סמך מידע שיש להם על מי שמשתמשים באתר. אנשים במספרים עצומים צופים בסרטים ובסדרות בנטפליקס, והחברה מתעדת את כל הרגלי הצפייה שלהם. במילים פשוטות, פירוש הדבר שבנטפליקס יודעים באילו סוגי סרטים וסדרות אנחנו צופים, בין שאלה סרטים דוקומנטריים העוסקים באלגוריתמים לתכנון מסלולים, ובין שאלה סרטי אימה או כל סגנון אחר. בנטפליקס גם מסווגים את כל הסרטים ואת כל הסדרות שלהם לקטגוריות, ומשתמשים בשתי סדרות נתונים כדי להפיק את ההמלצות שלהם. אם אתם צופים בסרטי אימה רבים, בוודאי תרצו לצפות בעוד סרט כזה שעדיין לא צפיתם בו. נשמע די פשוט בסופו של דבר.

הקושי טמון בדברים אחרים הנעשים בנטפליקס. הם מקצים לכל הסרטים ולכל הסדרות שאינם משתייכים בבירור לקטגוריה מסוימת, כגון סרטי אימה, ניקוד שניתן באחוזים. הניקוד באחוזים מראה עד כמה הסרט מתאים לסרטים שאתם צופים בהם בדרך כלל. במילים אחרות, בנטפליקס מחליטים עד כמה סרט הרפתקאות דומה לסדרה של סרטי אימה. אם מתרחשים בו הרבה דברים מפחידים נורא, הוא יתאים בצורה טובה יותר להרגלי הצפייה שלכם מאשר סרט שאין בו הרבה התרחשויות כאלה. אלה הם פרטים מהסוג שהחברים שלכם מספרים לכם כשאתם מבקשים מהם להמליץ על משהו שכדאי לכם לצפות בו. גם נטפליקס יכולים לספק לכם את המידע הזה, אם כי ההמלצות שלהם אינן מתקרבות ברמת הדיוק שלהן לאלה של משוגע אמיתי לסרטים.

המצב מסתבך יותר במקרה שבהם אתם מעדיפים סרטי אימה רק מסוג מסוים. אם אינכם אוהבים את אלה המדממים, סרטים עתירי דם לא יתאימו לפרופיל שלכם באותה מידה כמו סרט הרפתקאות המפחיד מעט מעל הממוצע. בחינה של סרטים מקטגוריה כללית מסוימת לא תספק לכם את ההמלצות הקולעות ביותר, מאחר שהדבר החשוב באמת הוא תוכן הסרט. מאחר שמחשבים אינם יכולים להבין תוכן, ייתכן שחברת נטפליקס צריכה להעסיק צוותים רבים שמבינים תכנים. אבל מאחר שיש לה מיליוני צופים, אין היתכנות לפתרון כזה, ובחברה נאלצים להסתפק במחשבים ובאלגוריתמים להפקת ההמלצות שלהם. אפשר לעשות זאת, אבל נחוץ כאן טריק.

הרעיון עצמו פשוט למדי: המלצה נחשבת טובה אם היא דומה למה שאתם אוהבים לצפות בו. אנשים בכל העולם צופים בתוכניות של נטפליקס שהם מחבבים כי הן דומות לסדרות ולסרטים שהם צפו בהם בעבר. עבור המחשבים של נטפליקס, שני סרטים נחשבים דומים זה לזה אם אנשים רבים שראו אחד מהם צופים גם בשני. אם אלפי אנשים צופים בסרט ״איירון מן 2״ אחרי שצפו ב״איירון מן״, הם מן הסתם דומים, ו״איירון מן 2״ הוא המלצה טובה לאנשים שצפו ב״איירון מן״. ככל שאנשים רבים יותר משתמשים בנטפליקס, כך החיזויים של נטפליקס ייעשו מדויקים יותר. התוכנה מציעה סדרות וסרטים שאנשים רבים מאוד כבר צפו בהם ושהם דומים או זהים בקירוב למה שאתם צפיתם בו.

אבל הפתרון הזה כרוך בבעיה. לנטפליקס יש מיליוני משתמשים, וכל אחד מהם צפה במספר גדול של סרטים ושל סדרות. הטריק שמשתמשים בו בנטפליקס כדי להציע את ההמלצות שלהם הוא חישוב מתמטי פשוט: התוכנה בודקת כמה אנשים שיש להם אותה היסטוריית צפייה — צפו גם בתוכנית שהיא רוצה להמליץ עליה. הבעיה היא בחישוב. אני מסביר אותה כאן בצורה פשוטה משום שהפרטים אינם חשופים לציבור. נטפליקס צריכים להביא בחשבון גם אנשים שראו כמעט, אבל לא בדיוק, את אותן תוכניות. ומה בדבר אנשים שאוהבים למשל לא רק סרטי אימה אלא גם סרטים תיעודיים? אם כך, יש הרבה פחות אנשים שצפו בדיוק באותן תוכניות, והעובדה הזאת עושה את ההמלצות מהימנות פחות. הרעיון הפשוט מתגלה כמסובך למדי ליישום.

זו הסיבה לכך שהצגת הסרטים והתוכניות הזמינים על מפה, כמו זו של הרכבת התחתית, עשויה לעזור בפתרון הבעיה. כל סרט או סדרה הם מעגל, כמו תחנה בעולם של נטפליקס. אפשר לנסוע מתחנה לתחנה על ידי בחירה בשני סרטים שונים או בשתי סדרות שונות באתר של נטפליקס.

גם על המפה הזאת יש להוסיף מספרים כדי שאפשר יהיה לחשב את ההמלצות. המספרים אינם מייצגים זמני נסיעה, אלא את מספר האנשים שצפו בשתי תוכניות המחוברות בקו. אפשר לראות דוגמה פשוטה מאוד בתרשים הבא, המתאר שלושה סרטים ומספרים דמיוניים המציינים כמה אנשים צפו בהם, בצירופים שונים:

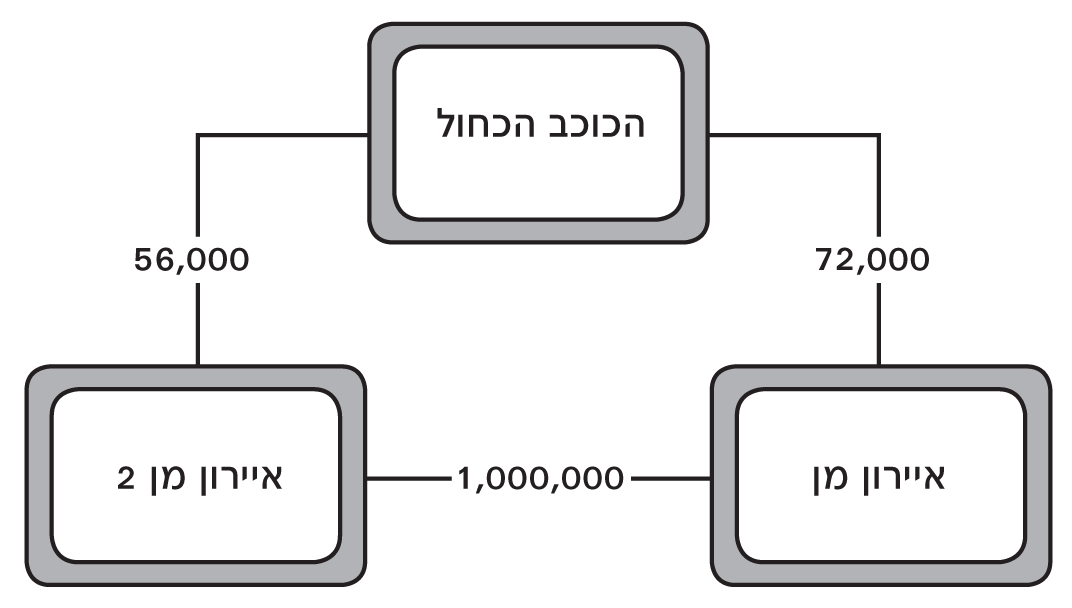
נטפליקס: מספרי צפייה בדויים עבור שלושה סרטים

השאלה היא: איזה אחוז יקבל כל סרט, כך שיעיד עד כמה הוא מתאים להתנהגות הצפייה של כל אחד מכם? נניח שמישהו צופה בנטפליקס רק ב״איירון מן״. המחשב צריך לחזות עד כמה הוא יאהב את ״איירון מן 2״ וגם את ״הכוכב הכחול״. לפי התרשים, ״איירון מן 2״ יקבל אחוז גבוה מאוד. הרי יש סיכוי גדול הרבה יותר שתיהנו מסרט שצפו בו אנשים רבים החולקים איתכם אותו טעם בסרטים. ״הכוכב הכחול״, לעומת זאת, יקבל ניקוד נמוך יותר, שכן רק מעט אנשים שצפו בו צפו גם ב״איירון מן״. יתרה מזו, רק אנשים מעטים שצפו ב״איירון מן 2״ (אשר המחשב סבור שהוא לטעמכם) צפו גם ב״כוכב הכחול״ — סיבה נוספת להעניק לו ניקוד נמוך באחוזים.

השורה התחתונה היא שהמחשב משתמש בחיזויים שלו עצמו — לדוגמה, עד כמה תיהנו מ״איירון מן 2״ — כדי לשפר את החיזויים שלו לגבי סרטים וסדרות אחרים. לא קשה לעשות זאת כשמדובר בשלושה סרטים בלבד, אבל נסו לעשות זאת עם אלפי סרטים וסדרות. הדבר אפשרי בתיאוריה; אם יש לכם זמן ומקום בכמות מספקת, אתם יכולים למצוא בעצמכם כל מסלול שתרצו לנסוע בו. אבל הודות למתמטיקה, ובעיקר בזכות הגרפים שנתבונן בהם בפרק 7, הדבר אפשרי לא רק בתיאוריה אלא גם הלכה למעשה, כמובן אם יש לכם מחשב חזק די הצורך. הגרסה המתמטית של החידה הזאת מאפשרת לנטפליקס לחזות באופן אוטומטי לחלוטין אם תיהנו מסדרה או מסרט מסוים מבלי להיעזר בצבא של משוגעים לסרטים.

מתמטיקה בכל מקום
אנחנו נתקלים במתמטיקה מדי יום ביומו, ובכל מיני מקומות. לא פשוטו כמשמעו, כמובן. אפילו אני איני צריך לחשב חישובים מתמטיים ביום רגיל, גם אם זו העבודה שלי — לחשוב על מתמטיקה. ועם זאת, מאחורי הקלעים המתמטיקה ממלאת תפקיד מרכזי בחיינו. בלעדיה לא יהיו מפות גוגל שיראו לנו את הדרך; נטפליקס יוכלו להציע לנו כמה סרטים וסדרות באקראי, שאולי תיהנו מהם, אבל הם יהיו מכֻוונים הרבה פחות לטעמכם; מנוע החיפוש של גוגל כמעט לא יוכל לעבוד. בקצרה, שירותים שאנחנו משתמשים בהם מדי יום ביומו יכולים לפעול רק משום שהם משתמשים במתמטיקה, גם אם אינכם רואים אותה.

נטפליקס, מנועי חיפוש ותוכנות לתכנון מסלולים הם דוגמאות לשירותים שתלויים באותו ענף של המתמטיקה: תורת הגרפים. אבל אין זה התחום היחיד במתמטיקה שיש לו חשיבות בחיי היום־יום. ידיעות חדשותיות רבות שקופצות לכם בטלפון מכילות סטטיסטיקה. סקרים לקראת בחירות מתיימרים להציג את ההעדפות של הבוחרים במדינה שלמה כסדרה של מספרים. אבל עד כמה הם מועילים? הם יכולים להיות רחוקים מאוד מהתוצאות, כפי שראינו בבחירות לנשיאות ארצות הברית בשנת 2016. לפי הסקרים הילרי קלינטון היתה צפויה לנצח, וכמה מהמומחים אפילו טענו שהם בטוחים כמעט במאה אחוז בתוצאה. מִספרים יכולים להטעות בקלות, גם אם הדבר לא נעשה בכוונה תחילה. נתונים סטטיסטיים מסתירים כל מיני דברים. עבור מי שאינו מבין מה יכול להשתבש, נתון סטטיסטי שנראה חשוב הוא למעשה חסר תועלת. אמנם הסקרים אומרים לכם משהו, אבל איך תוכלו לבטוח בהם כאשר הם שוגים לעתים קרובות כל כך?

אתם מרימים לרגע את המבט מהנייד שלכם כדי להזמין אספרסו. הקפה נעשה במכונת קפה מפלדה בוהקת שמחממת את המים בדיוק לטמפרטורה הנכונה. אם המכונה היא מדגם יוקרתי, זה לא קורה סתם כך. המכונה מנטרת את מהירות ההתחממות של המים, ועל סמך המידע הזה מחליטה אם צריך לחמם אותם עוד קצת או להניח להם להצטנן, וכך הלאה. המכונה עושה זאת עד שהמים מגיעים לטמפרטורה המושלמת הדרושה להכנת הקפה. אינכם רואים את כל התהליך הזה, אבל ממש מול האף, הנוסחאות המתמטיות שהמורה שלכם דיברה עליהן בכיתה משמשות להכנת הקפה שלכם.

בזמן שאתם שותים את האספרסו, אתם קוראים את החדשות הפוליטיות בעיתון. הממשלה שינתה כמה נושאים במדיניות שלה. אתם לא בטוחים שזהו רעיון טוב, לכן אתם מעיפים מבט בתחזיות לגבי התוכניות החדשות. כתמיד, מכוני מחקר העוסקים בכלכלה ניתחו את התוכניות על כל פרטיהן. השאלה אם רעיון כלשהו הוא טוב או רע תלויה בגורמים רבים כל כך, שאתם מתקשים לעקוב אחריהם. אבל חישוב אחד מצרף את כל הגורמים האלה לפיסת מידע אחת, והיא זו שחשובה לכם: האם בסופו של דבר יהיה לכם יותר, או פחות, כסף בכיס.

כשאנחנו מסתכלים כך על הדברים, אנחנו רואים כי למתמטיקה יש השפעה גדולה על חיינו. אנחנו תלויים במספר גדול מאוד של חישובים מבלי שנעשה אותם בעצמנו. המידע המשמש אותנו בעת שאנו מקבלים החלטות הוא תוצאת הקצה של עבודה מתמטית רבה שנעשית על ידי אחרים. אפילו המידע שאתם זוכים לראות בעצמכם בסופו של דבר תלוי בחישוב שנעשה אי־שם במחשב שמשמש את גוגל, את פייסבוק או כל אתר רשת אחר שמסנן נתונים. הטכנולוגיה המקיפה אותנו מכל עבר משתמשת במתמטיקה במידה הולכת וגדלה. לא רק מכונת הקפה היוקרתית של בית הקפה הפינתי, גם הטייס האוטומטי במטוס שלוקח אתכם לחופשה שלכם, או המחשב שאתם משתמשים בו מדי יום ביומו בעבודתכם — כולם תלויים במתמטיקה. מאחר שהשימושים במתמטיקה נמצאים בכל מקום סביבנו, יש חשיבות רבה לכך שנבין אותה טוב יותר, ושנבין גם את האופן שבו היא משפיעה על חיינו.

זהו הדבר העיקרי שהספר עוסק בו: מה יועיל לנו אם נדע משהו על מתמטיקה. אבל מהי המתמטיקה ואיך היא פועלת? השאלה הזאת היא בראש ובראשונה שאלה פילוסופית, ותחילתה מעוגנת בעבר הרחוק, בזמנם של סוקרטס ושל אפלטון. הם שאלו את עצמם מהי המתמטיקה, במה היא עוסקת ואיך אנחנו יכולים ללמוד ולדעת אותה. יתר על כן, אם תחשבו על כך לרגע, יש משהו מוזר בעובדה שיש למתמטיקה יישומים מעשיים נרחבים כל כך, ועם זאת היא כה מופשטת. איך ייתכן שהיא מועילה כל כך? כדי לענות על השאלה הזאת נצטרך לפנות לפילוסופיה.